Jupiters you seek?
Find massive, metal-rich stars
Planets you will find!
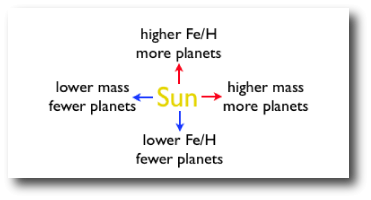The diagram is from Greg Laughlin's oklo.org. I made up the haiku last night. Both pretty much summarize the major results of my latest paper, written with coauthors Kimberly Aller (just-graduated UCB physics/astro major and my REU summer student at U. Hawaii last year), Andrew Howard (UCB Postdoc and planet-hunter extraordinaire), and Justin Crepp (Caltech postdoc, statistics and high-contrast imaging expert).
The dependence of giant planet "occurrence" (where and how often we find gas-giant planets) was the focus of my thesis work at UC Berkeley. I expanded the mass range of our planet search by including "retired" massive stars in our survey. Massive stars are normally rapid rotators, which smears out their spectra and makes them difficult planet-search targets. But when stars get old enough to run out of hydrogen, they move into retirement, which causes them to slow down and become better-behaved targets.
By measuring the fraction of target stars with planets (number of planet-hosts divided by total number of stars), in 2007 I published this plot:
This showed a general trend: massive stars have more planets than low-mass stars. However, by dividing the stellar sample into these broad bins, we couldn't see the underlying form of the relationship. Does the planet fraction rise exponentially? Linearly? Does it turn over?
When I went to Hawaii as a postdoc, I enlarged my sample of retired massive stars by using the larger, Keck telescope. By tripling my sample size I hoped to eventually get a clearer picture than the one we had in 2007.
Last summer, UCB undergraduate astrophysics student Kimberly Aller visited the Institute for Astronomy at the University of Hawaii to do a summer project with me. I started Kimberly off on an small project that she quickly devoured in about two weeks. So I decided to give her a larger, more challenging project: Measure the functional form describing planet occurrence as a function of stellar mass. Oh, and she had to take into account the known effects of stellar metallicity.
Metallicity is a measure of the amount of heave elements in a star's atmosphere. Astronomers call everything heavier than helium a "metal," and for stars we use the amount of iron as a proxy for all of the other "heavy" elements. Debra Fischer and Jeff Valenti showed that stars with heavy metals are far more likely than metal-deficient stars to harbor a giant planet.
So Kimberly used the method of Bayesian inference to simultaneously measure the effects of mass and metallicity on planet occurrence among a sample of 1194 target stars with masses ranging from 20% the mass of the Sun up to twice the Sun's mass. Many thanks to Mike Fitzgerald for originally pointing out this method, way back in 2005! One of the huge advantages of the method is that we don't have to bin the data, which allows us to sense the underlying relationship much more sensitively.
Here's the main figure:
The gray line shows the measured fraction of stars with planets, as a function of stellar mass. The red line is the prediction from our best-fitting model, which accounts for both mass and metallicity. The blue line shows the underlying stellar mass relationship, which is almost exactly linear. The picture is much clearer now!
Kimberly did such a good job developing and implementing the methodology that I decided we needed to publish our results ASAP!
Well, ASAP turned into almost a year later and resulted in a much longer paper than I had originally planned. One reason is that I moved and started a new job right after the summer ended! The other reason for the delay is that this is a pretty important result and I wanted to make sure as possible that we are correct. Andrew Howard helped me check and recheck our planet detections and the targets we used in our analysis. Justin Crepp took our model for a "test drive" and uncovered a couple of major flaws in our early draft. I also received a lot of feedback from the community after giving talks presenting our results and sharing the preprint of our paper. Science in action!
There are two reasons why this result is important. First, it tells us where to look for more planets (hence the haiku above). Second, this result gives us important clues about how planets form. Theoretical models of planet formation must produce more planets around massive, metal-rich stars. In the paper we argue that this implies a bottom-up formation process, whereby Jupiter-like planets start from the collisions of little dust grains, which turn into boulders, then Earth-sized bodies, which then sweep up massive amounts of gas to result in a gas-giant planet with a solid core.
As for where to look for planets, my postdoc Justin Crepp is nearly ready to submit our paper on where to find the next "photogenic" planets! More on that later...
For now, I'm off to our daily, department astro-ph discussion!
Find massive, metal-rich stars
Planets you will find!
The diagram is from Greg Laughlin's oklo.org. I made up the haiku last night. Both pretty much summarize the major results of my latest paper, written with coauthors Kimberly Aller (just-graduated UCB physics/astro major and my REU summer student at U. Hawaii last year), Andrew Howard (UCB Postdoc and planet-hunter extraordinaire), and Justin Crepp (Caltech postdoc, statistics and high-contrast imaging expert).The dependence of giant planet "occurrence" (where and how often we find gas-giant planets) was the focus of my thesis work at UC Berkeley. I expanded the mass range of our planet search by including "retired" massive stars in our survey. Massive stars are normally rapid rotators, which smears out their spectra and makes them difficult planet-search targets. But when stars get old enough to run out of hydrogen, they move into retirement, which causes them to slow down and become better-behaved targets.
By measuring the fraction of target stars with planets (number of planet-hosts divided by total number of stars), in 2007 I published this plot:
This showed a general trend: massive stars have more planets than low-mass stars. However, by dividing the stellar sample into these broad bins, we couldn't see the underlying form of the relationship. Does the planet fraction rise exponentially? Linearly? Does it turn over?When I went to Hawaii as a postdoc, I enlarged my sample of retired massive stars by using the larger, Keck telescope. By tripling my sample size I hoped to eventually get a clearer picture than the one we had in 2007.
Last summer, UCB undergraduate astrophysics student Kimberly Aller visited the Institute for Astronomy at the University of Hawaii to do a summer project with me. I started Kimberly off on an small project that she quickly devoured in about two weeks. So I decided to give her a larger, more challenging project: Measure the functional form describing planet occurrence as a function of stellar mass. Oh, and she had to take into account the known effects of stellar metallicity.
Metallicity is a measure of the amount of heave elements in a star's atmosphere. Astronomers call everything heavier than helium a "metal," and for stars we use the amount of iron as a proxy for all of the other "heavy" elements. Debra Fischer and Jeff Valenti showed that stars with heavy metals are far more likely than metal-deficient stars to harbor a giant planet.
So Kimberly used the method of Bayesian inference to simultaneously measure the effects of mass and metallicity on planet occurrence among a sample of 1194 target stars with masses ranging from 20% the mass of the Sun up to twice the Sun's mass. Many thanks to Mike Fitzgerald for originally pointing out this method, way back in 2005! One of the huge advantages of the method is that we don't have to bin the data, which allows us to sense the underlying relationship much more sensitively.
Here's the main figure:
The gray line shows the measured fraction of stars with planets, as a function of stellar mass. The red line is the prediction from our best-fitting model, which accounts for both mass and metallicity. The blue line shows the underlying stellar mass relationship, which is almost exactly linear. The picture is much clearer now!Kimberly did such a good job developing and implementing the methodology that I decided we needed to publish our results ASAP!
Well, ASAP turned into almost a year later and resulted in a much longer paper than I had originally planned. One reason is that I moved and started a new job right after the summer ended! The other reason for the delay is that this is a pretty important result and I wanted to make sure as possible that we are correct. Andrew Howard helped me check and recheck our planet detections and the targets we used in our analysis. Justin Crepp took our model for a "test drive" and uncovered a couple of major flaws in our early draft. I also received a lot of feedback from the community after giving talks presenting our results and sharing the preprint of our paper. Science in action!
There are two reasons why this result is important. First, it tells us where to look for more planets (hence the haiku above). Second, this result gives us important clues about how planets form. Theoretical models of planet formation must produce more planets around massive, metal-rich stars. In the paper we argue that this implies a bottom-up formation process, whereby Jupiter-like planets start from the collisions of little dust grains, which turn into boulders, then Earth-sized bodies, which then sweep up massive amounts of gas to result in a gas-giant planet with a solid core.
As for where to look for planets, my postdoc Justin Crepp is nearly ready to submit our paper on where to find the next "photogenic" planets! More on that later...
For now, I'm off to our daily, department astro-ph discussion!
Comments
Fascinating.
But I did send the post to Ben and he loved your explanation. He says, and I quote, "thank you for forwarding John's stuff. I thought it was fabulous. It's very impressive how good he is at explaining things." :)