A subwoofer agitates a stream of water at 24 +/- $\epsilon$ Hz, where $\epsilon \sim 1$, while video is recorded at a frame rate of 24 Hz (i.e. sub-Nyquist). Fun ensues!
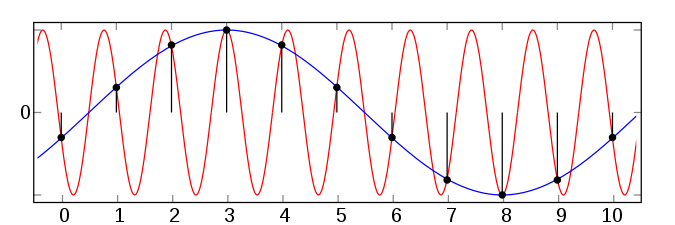
This effect is known as aliasing, which is also responsible for helicopter blades and car wheels appearing to spin backwards in films. Aliasing is also important in finding planets. We sample the radial velocity variations of stars caused by their planets using instruments such as HIRES at the Keck observatory. If we don't sample with dense enough time coverage (high enough frequency), a sub-sampled radial velocity signal can appear at a shorter or longer period. Here's an example from Wikipedia:
Imagine that the red curve is the true signal and the apparent (measured) signal is blue. You gotta mind your time-sampling! The optimal sampling is less than half the period (twice the frequency), which is known Nyquist samling.
This is what caused planet hunters (including me) to get the orbital period of 55 Cancri e wrong. Bekki Dawson and Dan Fabrycky found the correct signal at a much shorter orbital period than was previously thought. Since the planet was closer to the star, the probability that it would transit increased by a large amount (roughly a factor of 3, if memory serves). This prompted Josh Winn and collaborators to search for transits with a space telescope called MOST. And this is how the brightest transiting planetary system was discovered!
(The fuller story involves a prejudice against the existence of planetary periods less than 1 day, which caused our diagnostic periodogram plots to be plotted starting at 1. This hid the true period near 0.73 days, and drew attention to the aliased signal near 2.8 days. Other more technical details not suited for this blog are covered by Dawson & Fabrycky.)
This effect is known as aliasing, which is also responsible for helicopter blades and car wheels appearing to spin backwards in films. Aliasing is also important in finding planets. We sample the radial velocity variations of stars caused by their planets using instruments such as HIRES at the Keck observatory. If we don't sample with dense enough time coverage (high enough frequency), a sub-sampled radial velocity signal can appear at a shorter or longer period. Here's an example from Wikipedia:
Imagine that the red curve is the true signal and the apparent (measured) signal is blue. You gotta mind your time-sampling! The optimal sampling is less than half the period (twice the frequency), which is known Nyquist samling.
This is what caused planet hunters (including me) to get the orbital period of 55 Cancri e wrong. Bekki Dawson and Dan Fabrycky found the correct signal at a much shorter orbital period than was previously thought. Since the planet was closer to the star, the probability that it would transit increased by a large amount (roughly a factor of 3, if memory serves). This prompted Josh Winn and collaborators to search for transits with a space telescope called MOST. And this is how the brightest transiting planetary system was discovered!
(The fuller story involves a prejudice against the existence of planetary periods less than 1 day, which caused our diagnostic periodogram plots to be plotted starting at 1. This hid the true period near 0.73 days, and drew attention to the aliased signal near 2.8 days. Other more technical details not suited for this blog are covered by Dawson & Fabrycky.)
Comments